Research - Olivier Lefebvre

Research

Home

My research deals with path planning and trajectory execution for non-holonomic systems. In this work we have been interested in several topics of mobile robotics:

Path planning
Localization
Online collision detection
Non-holonomic path optimization in the context of :

obstacle avoidance
docking

Trajectory following with localization discontinuities

Path planning Given a mobile robot with kinematic constraints and given a map of the environment, the problem is to compute a collision-free path that is feasible by the system. We use the software Move3D to solve this problem. More details on that topic can be found at this address.

A trajectory computed by Move3D using RRT algorithm (Rapidly-Exploring Random Tree)	A trajectory for Hilare2 with a trailer computed with PRM algorithm (Probabilistic Roadmap Method).

Collision at execution time		Top
The path planned in the model of the environment is collision-free. But collisions can occur at execution time, for several reasons: imprecision in the model of the environment poor localization of the robot unexpected obstacles

Map imprecision : an obstacle was not correctly modeled in the map. The planned trajectory is in collision with this obstacle.	Bad localization : sensor perception (red dots) does not match the map. Thus, a collision- free trajectory in the map (in blue) is in collision in the reality.	Unexpected obstacle: an obstacle which was not in the model used for planning lies on the trajectory
The localization process fuses odometry data and feature based localization data, to obtain a minimum variance position estimate. A document in French explains the approach.
Obstacles interactions (collision checking, repulsive potential) with the trajectory must periodically be computed. An article [4] presents some optimizations of these computations.

Reactive obstacle avoidance	Top
Recently we have developed a Non-Holonomic Path Deformation method. It enables the robot to reactively adapt its trajectory at execution time when collisions are detected. The trajectory is deformed in order to get away from obstacles while keeping the non-holonomic constraints satisfied. It has been implemented and tested on several robots. More details on that topic can be found at this address.

The non-holonomic path deformation method has been implemented on robot CyCab, from INRIA Rhone-Alpes. (AVI 5724 Ko, MP4 3614 Ko).
An article [2] presents the implementation of the method on robot CyCab. The method has been implemented on other robots: ATRV rover Dala (MOV 3450 Ko, MP4 4214 Ko), and others here. The article [3] that presents the non-holonomic deformation method has received the "2004 King-Sun Fu Memorial Best Transactions on Robotics Paper Award" of the IEEE Robotics and Automation Society.

Docking for non-holonomic systems	Top
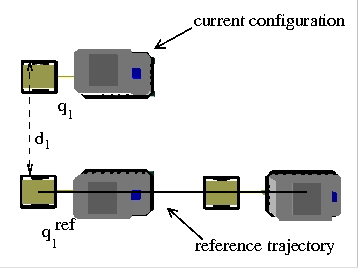
Precise parking for non-holonomic systems in cluttered environments is a very challenging issue. Kinematic and environment complexity make fast path re-planning impractical. We have used the Non-Holonomic Path Deformation method in this context. We deform a planned trajectory so that it reaches a docking configuration defined as a desired sensor perception. The robots avoids obstacles at the same time.
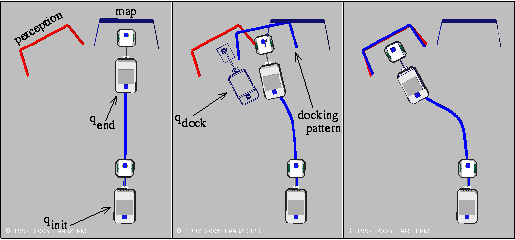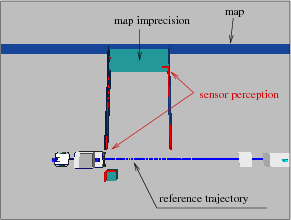
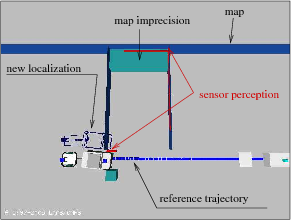
	The docking configuration is defined as the position of the sensor where the actual sensor perception best matches the desired sensor perception (called docking pattern). Notions are similar to those of visual-servoing.
Some movies of docking tasks with a SICK sensor:	(we use GDHE for the 3D real-time display of robots data)
Simulated environment robot CyCab in a parking: MP4 2010 Ko. robot Hilare2 towing a trailer, backward: AVI 398 Ko. robot Hilare2 with a trailer, parking in an imprecisely defined parking lot: AVI 559 Ko. robot Hilare2 with a trailer, parking between 2 boxes, with undefined positions and width: AVI 516 Ko, AVI 503 Ko, AVI 658 Ko. robot Hilare2 with a trailer, in a parking lot with 2 SICK sensors: AVI 593 Ko.
Real Experiments	Some videos are time rescaled
Robot Hilare2 with a trailer, with a docking pattern defined relatively to the trailer, parking: between 2 boxes (MP4 2790 Ko). between the boxes again, but this time they are shifted when the robot can not see them (MP4 5006 Ko). then going under a desk (MP4 5433 Ko). then between the boxes again (MP4 5463 Ko). then coming back under the desk, which is shifted when the robot can not see it (MP4 5806 Ko). finally, precise parallel parking with respect to the trailer (MP4 5289 Ko).
A document in French presents the notions of likelihood and of Mahalanobis distance, which are commonly used in estimation. In the context of a docking task, we use these notions to find the docking pattern among the perceived features and to evaluate the likelihood of the docking position compared to the planned final configuration. The paper [5] presents this work.

Integration of localization, trajectory following and collision detection		Top
Following a trajectory while localizing and avoiding obstacles is not as simple as it seems, when dealing with multi-body vehicles. Landmark-based localization can produce discontinuities of the robot position estimation, as it is well known with GPS systems, and perturb the trajectory following. If the robot is able to converge smoothly towards the trajectory it follows, then these perturbations are easily managed. Otherwise, if the robot is more complex (for instance a multi-body mobile robot subject to several nonholonomic constraints) and navigates in a cluttered environment, these perturbations can lead to collisions.
For a robot towing a trailer, the distance to the reference trajectory may increase before decreasing when catching up with the reference trajectory.
Due to this convergence property, a discontinuity in the localization can lead to a collision. In the example below, the localization discontinuity is due to an obstacle which is matched with a landmark (a segment in this case) of the map. We have reproduced this case in a realistic simulation environment (AVI 540Ko)

The robot follows the trajectory and is consistently localized	The robot localization changes suddenly because an obstacle is matched with a landmark of the map	While catching up with the reference trajectory, the robot hits an obstacle that it had no time to avoid
We have a proposed a solution to this problem. The idea is take into account the effect of the localization discontinuity further on the reference trajectory. Then the catching up is not performed immediately but is simulated at a certain distance on the trajectory, so that the trajectory effectively executed by the robot is always checked for collision beforehand. The same trajectory as before is now executed with the new algorithm running (AVI 1220Ko), and it is performed without collision in spite of the discontinuities of the localization. The paper [7] presents a formal statement of the problem and details the algorithm for safe trajectory following.

Last Modified: December 27th, 2006